Zero To One and The Black Swan
Connecting the dots on fractals, outliers, power law distributions and beyond
When I first read Gödel, Escher, Bach about a year ago, it left me ablaze with a vast range of open questions, one of which was, where does meaning reside? In the message or in the recipient?
Since then, I’ve come to develop a two-layer model for differentiated insights:
Δ insights = (Δ consumption of content) x (Δ interpretation)
Δ consumption of content might relate to reading obscure rather than mainstream books, or consuming academic papers/podcasts/articles that others aren’t.
Δ interpretation is evident in the thought experiment that if Warren Buffett and I both read the same annual report, the Oracle of Omaha will glean far more insights.
In the spirit of Δ interpretation, I am sharing my understandings and interpretations from reading Peter Thiel’s Zero To One and Nassim Nicholas Taleb’s The Black Swan. While reading these books and thinking through their ideas, I had a number of insights from connecting the dots that I will elaborate in this post.
Quine’s Infinity of Interpretations
As it turns out, The Black Swan itself touches on this idea — logician W. V. Quine suggested that for any given set of facts, there could be an infinity of possible interpretations by different thinkers (somewhat like quantum mechanics, where interpretations range from Copenhagen to many worlds).
The Black Swan then points out the paradox that Quine’s hypothesis can itself be interpreted in infinitely many ways: “Note here that someone splitting hairs could find a self-cancelling aspect to Quine’s own writing. I wonder how he expects us to understand this very point in a noninfinity of ways.”
When I read this, I thought back to my favourite book, Gödel, Escher, Bach, which has a chapter (number VI) entirely on such ideas, and which argues for the universality of at least some messages. The Black Swan seems to agree:
Consider that two people can hold incompatible beliefs based on the exact same data. Does this mean that there are possible families of explanations and that each of these can be equally perfect and sound? Certainly not. One may have a million ways to explain things, but the true explanation is unique, whether or not it is within our reach.*
Thus, going back to my pseudo-equation above, in a message that has a single objective meaning, Δ interpretation = 0, hence Δ insights = 0. This may be a possible solution to the paradox inherent in Quine’s statement.
*If you are intrigued by this notion of explanations, I would recommend reading The Beginning of Infinity by David Deutsch.
The Future is Δ
Reductionism is an approach that seeks to explain everything in terms of fundamental rather than higher-level emergent explanations.
For example, consider one particular copper atom at the tip of the nose of the statue of Sir Winston Churchill that stands in Parliament Square in London. Let me try to explain why that copper atom is there. It is because Churchill served as prime minister in the House of Commons nearby; and because his ideas and leadership contributed to the Allied victory in the Second World War; and because it is customary to honour such people by putting up statues of them; and because bronze, a traditional material for such statues, contains copper, and so on.
Thus we explain a low-level physical observation — the presence of a copper atom at a particular location — through extremely high-level theories about emergent phenomena such as ideas, leadership, war and tradition. There is no reason why there should exist, even in principle, any lower-level explanation of the presence of that copper atom than the one I have just given.
Presumably a reductive ‘theory of everything’ would in principle make a low-level prediction of the probability that such a statue will exist, given the condition of (say) the solar system at some earlier date. It would also in principle describe how the statue probably got there.
But such descriptions and predictions (wildly infeasible, of course) would explain nothing. They would merely describe the trajectory that each copper atom followed from the copper mine, through the smelter and the sculptor’s studio, and so on. They could also state how those trajectories were influenced by forces exerted by surrounding atoms, such as those comprising the miners’ and sculptor’s bodies, and so predict the existence and shape of the statue.
In fact such a prediction would have to refer to atoms all over the planet, engaged in the complex motion we call the Second World War, among other things. But even if you had the superhuman capacity to follow such lengthy predictions of the copper atom’s being there, you would still not be able to say, ‘Ah yes, now I understand why it is there.’
— David Deutsch, in The Fabric of Reality
Likewise, a reductionist view of the future suggests that it is merely the set of temporal coordinates that have not yet occured. However, a more deep and interesting explanation is that the future is a time different from the present.
The future is interesting not because it hasn’t happened yet, but because it will be different from the present.
The Contrarian Question
Peter Thiel poses his famous contrarian question: What important truth do very few people agree with you on?
Good answers to the contrarian question are as close as we can come to looking into the future. (More on this soon.)
The Axes of Progress
There are two axes along which progress occurs: vertical (0 to 1) and horizontal (1 to n). These axes are orthogonal — i.e., perpendicular — which means that no component of one lies along the other (their dot product is zero). Simply put, vertical and horizontal progress are independent; “what got you here won’t get you there.”
This paradigm comes up in various domains:
Economics, where developing economies (0 to 1) often adopt protectionism, which is disdained by developed economies (1 to n) who ‘kick away the ladder’ and prescribe one-size-fits-all policies. [I recommend reading Joe Studwell’s excellent book How Asia Works if you are interested in this.]
Performance psychology, where deliberate practice is required to attain hard new skills (0 to 1), while a flow state is experienced when repeating what one is already proficient at (1 to n). [Cal Newport’s wonderful podcast with Andrew Huberman has a debate on deliberate practice v/s flow — my understanding is they correspond to 0 to 1 and 1 to n respectively, and are therefore orthogonal.]
Those managing large family offices, endowments or pension funds are often incentivised to preserve capital (1 to n), as opposed to, say, an individual angel investor, who seeks to grow it at a rapid rate (0 to 1).
Terminal Value
When Peter Thiel ran some projections in 2001, he realised that 75% of PayPal’s value would come from cash flows generated after 2011, i.e., terminal value.
Similarly, when Elon Musk says that he expects Optimus to drive the majority of Tesla’s long term value, it is terminal value to which he is referring.
Terminal value is driven by growth and durability — the compounding formula is driven by rate of return (growth) and longevity of time period (durability).
While most analysts focus on short-term growth, the more important question to ask is, ‘will this firm be around 10 years from now?’ The best answers to this question arise not by crunching numbers on a spreadsheet but through an understanding of intangibles — especially enduring intangibles like people and culture. [One of the best ways to appreciate this point is to read The Founders by Jimmy Soni, a book about PayPal’s founding story — or my interview with the author and my post about scenius that touches on PayPal’s hiring methods, among other things.]
Proving Popperian Falsification
Karl Popper is often credited with the idea of falsification, namely that a hypothesis can never be confirmed but only ever disconfirmed. No number of spottings of white swans is sufficient to confirm the statement ‘all swans are white’, but a single sighting of a non-white swan is sufficient to disconfirm (falsify) it.
I had come this idea across a number of times, most notably in David Deutsch’s The Beginning of Infinity and in George Soros’ writings. While the idea of falsification is intuitively obvious, The Black Swan helped me gain deeper insights into a proof of the idea, which I detail here.
First, consider that the statement ‘all swans are white’ is logically equivalent to its contrapositive statement ‘all non-white objects are non-swans’ — which in turn can be rephrased as ‘the set of all non-white objects does not contain swans’.
For intuition, one can think of the contrapositive as a mathematical inequality: when both sides are multiplied by a negative number or when the reciprocal of both sides is taken (the or here is exclusive), the inequality sign is flipped. For instance, 5 > 3, but 1/5 < 1/3.
Hence, if it is true that the spotting of a white swan constitutes evidence for the validity of ‘all swans are white’, then it is also true that the spotting of a non-white non-swan (say, a red car) constitutes evidence for the validity of ‘all swans are white’. The latter is clearly erroneous, hence the Popperian idea of falsification is proven via reductio ad absurdum — QED.
Note how the above reasoning has not confirmed falsification itself, but disconfirmed its opposite — a proof by contradiction. Even falsification itself cannot be confirmed — this is akin to how a fallibilist must question fallibilism itself, or how a skeptical empiricist must doubt skeptical empiricism itself.
I would rather have questions that can’t be answered than answers that can’t be questioned.
— Richard Feynman
Kolmogorov Complexity
Suppose I send you a message of information value, say, one million bits, and you wish you further transmit this message to person X. If the characters in the message are perfectly random (such that the message makes no sense to a human), your transmitted message must also necessarily contain one million bits.
However, suppose now that the message I send you — again with a million bits — has the phrase ‘Black Swans are asymmetric’ typed out 50 times. In this case, your message to person X could simply type the phrase once and include a rule for repeating it 50 times. Hence, the message you transmit to person X contains much fewer than a million bits.
This phenomenon is termed Kolmogorov complexity, after Andrey Kolmogorov. The insights here are plentiful.
First, notice how Kolmogorov complexity is intensely dynamic, which means that an arbitrarily long, convoluted message (say, 200 pages long) that is seemingly random (high complexity) can, with the addition of a single suitable sentence, make complete sense.
This extra phrase may be, for example, a key to decrypt the message, or context that helps make sense of it. In such a case, complexity plummets instantly — and, somewhat counterintuitively, even though the extra sentence adds information (bits), it reduces the Kolmogorov complexity of the message as a whole.
This first point is similar to the idea of data compression.
Imagine six animated people having dinner around a table; they are deeply engrossed in a common discussion about, say, a person not there. During one moment of this discourse about Mr. X, I look across the table at my wife and wink. After dinner, you come up to me and say, “Nicholas, I saw you wink at Elaine. What did you tell her?”
I explain to you that we had dinner with Mr. X two nights before, at which time he explained that, contrary to __ he was in fact __, even though people thought __, but what he really decided was __ etc. Namely, 100,000 bits (or so) later, I am able to tell you what I communicated to my wife with 1 bit (I ask your forbearance with my assumption that a wink is 1 bit through the ether).
What is happening in this example is that the transmitter (me) and the receiver (Elaine) hold a common body of knowledge, and thus communication between us can be in shorthand. In this example, I fire a certain bit through the ether and it expands in her head, triggering much more information. When you ask me what I said, I am forced to deliver to you all 100,000 bits. I lose the 100,000-to-l data compression.
— Nicholas Negroponte, in Being Digital
Second, the parallels to computer code are plentiful. Consider how, in the case of the second message, a FOR loop can replace repeated PRINT functions, thus making the code succinct. In some sense, therefore, there exists a correspondence between Kolmogorov complexity and the maximal compactness of a computer program (an isomorphism, as GEB fans would call it).
Type I and II errors
“The power law means that differences between companies will dwarf the differences in roles inside companies.” Hence, participating in the ones that will create value is crucial. Put differently, when it comes to betting on outliers, mistakes of omission (type I) are much more expensive than mistakes of commission (type II).
The nature of the argument being made here is very similar to one that comes up often in math and physics:
Mass of string << mass of weights in a pulley system
Radius of earth >> height of a building
In such scenarios, the limiting case is often of great interest. The limit as x tends to infinity of (ln x / x) equals zero, for instance.
Connecting the dots, one can see that outlier bets premised on the power law distribution (0 to 1) are orthogonal to evolutionary biology (1 to n) — the former seeks to minimise Type II errors while the latter seeks to minimise Type I errors.
Natural selection among animals is incessant and merciless and has produced millions of species, all of whom adhere to this simple principle: Minimize the risk of committing type I errors to curtail the risk of injury or death, and learn to live with type II errors or foregone benefits.
— Pulak Prasad, in What I Learned About Investing from Darwin
Likewise for Black Swans — since they are so rare and impactful, Type I errors (omission) are costlier than Type II errors (commission).
Reverse Turkey
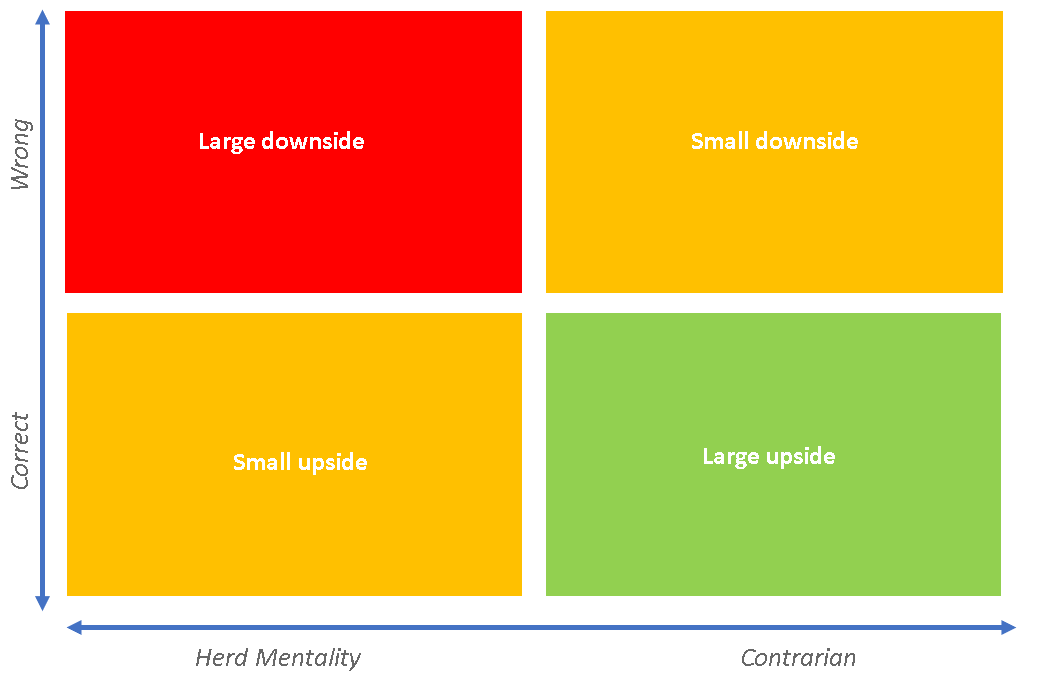
In some sense, connecting the dots with Zero To One, the reverse turkey idea is attempting an answer to the contrarian question, effectively saying: “Most people think Black Swan outliers can be safely ignored because they are not representative of the average, but the reality is that they drive the vast majority of outcomes in Extremistan.”
When betting that a Black Swan will occur, one is effectively being contrarian, risking a very-likely-but-small downside in pursuit of a highly-improbable-but-potentially-massive upside. Remember that a Black Swan is relative to expectations, so if a given event is to be a potential Black Swan, its complement (in set theory terms) must necessarily be “priced in” or “factored in”; hence, the non-occurence of the Black Swan does not create surprise, and therefore does not lead to a large downside. On the other hand, the occurence of the Black Swan does create surprise (by definition, since a Black Swan is relative to expectation), and hence promises a large upside if it materialises.
This framework supports Nero’s “bleed” strategy.
… Nero engaged in a strategy that he called “bleed.” You lose steadily, daily, for a long time, except when some event takes place for which you get paid disproportionately well. No single event can make you blow up, on the other hand—some changes in the world can produce extraordinarily large profits that pay back such bleed for years, sometimes decades, sometimes even centuries.
However, always betting that the Black Swan will occur effectively amounts to blind contrarianism — being contrarian just for the sake of opposing the crowds. Isn’t that simply a form of calibrated herd mentality (following the crowd but with a negative coefficient), as Patrick Collison suggests? This remains an open question for me, and thoughts would be very welcome.
One possible solution I can think of is that the Collison idea does not incorporate asymmetry of payoffs while the Taleb idea does.
However, there must be alignment between such a strategy and its practitioner.
…some business bets in which one wins big but infrequently, yet loses small but frequently, are worth making if others are suckers for them and if you have the personal and intellectual stamina. But you need such stamina. You also need to deal with people in your entourage heaping all manner of insult on you, much of it blatant.
People often accept that a financial strategy with a small chance of success is not necessarily a bad one as long as the success is large enough to justify it. For a spate of psychological reasons, however, people have difficulty carrying out such a strategy, simply because it requires a combination of belief, a capacity for delayed gratification, and the willingness to be spat upon by clients without blinking. And those who lose money for any reason start looking like guilty dogs, eliciting more scorn on the part of their entourage.
The nature of the referred-to stamina is itself interesting: “The main tragedy of the high impact-low probability event comes from the mismatch between the time taken to compensate someone and the time one needs to be comfortable that he is not making a bet against the rare event.”
Essentially, the contrarian view needs to be held for a long period of time, while the compensation — the “extraordinarily large profits that pay back such bleed for years, sometimes decades, sometimes even centuries” — is paid out in an extremely short period of time.
This connects back to the idea of minimising omission errors: since the compensation is paid out in an extremely short time period, it is of paramount importance that one participates during this time.
Ludic Fallacy
The ludic fallacy is when ideal, model games with odds that can be mathematically computed (e.g., blackjack) are used to learn about probabilities in the messy real world (e.g., financial markets).
…organized competitive fighting trains the athlete to focus on the game and, in order not to dissipate his concentration, to ignore the possibility of what is not specifically allowed by the rules, such as kicks to the groin, a surprise knife, et cetera. So those who win the gold medal might be precisely those who will be most vulnerable in real life.
Viewed from a different angle, then, the Black Swan idea is another solution to the contrarian question, effectively saying: “Most analysts focus on ideal, Platonic, precise-but-inaccurate probability calculations, but the reality is that while probabilities are hard to ascertain and susceptible to the ludic fallacy, payoffs can be estimated with a much lower error rate.”
Incremental Conditional Probabilities
For a normally distributed variable like expected lifespan, the older you grow, the lesser your incremental expected time to live. At birth, one might expect to live till the age of 80. At 80, one might expect to live another 5 years; at 85, another 2 years, and so on.
For a power-law distributed variable, on the other hand, the reverse is true. The better a startup is performing, the better it is expected to perform going forward. The more delayed a project already is, the longer it will take to complete going forward. This idea, which might be familiar as as the Lindy effect, supports the adage ‘average up your winners’.
Hofstadter’s Law: It always takes longer than you expect, even when you take into account Hofstadter’s Law.
— Douglas Hofstadter, in Gödel, Escher, Bach
Betting on Black Swans
Let me now present my understanding of the conditions under which it pays to bet on Black Swans (assuming the stamina condition is satisfied). Consider the concept of expected value: the probability multiplied by payoff, summed over all possible events.
I am skeptical about precise, numerical calculations of expected value — for instance, computing the expected value of a stock by estimating the probability-weighted bull, base, and bear scenarios — since these are susceptible to the ludic fallacy. Such an approach works when the odds are well-established and known, but that is hardly the case in many emergent domains.
Having said that, the non-numerical idea of expected value provides an interesting explanation for the payoffs of betting on Black Swans.
First, consider the trivial statement that as the extremity of an event increases, its probability decreases. However, the rate at which this occurs differs greatly depending on the nature of the distribution.
For a normally distributed variable (Gaussian/bell curve), the probability of extreme events declines at an exponentially increasing rate. The probability of a 4-sigma event is twice that of a 4.15-sigma event; the probability of a 20-sigma event is one trillion times that of a 21-sigma event!
On the other hand, a power law distribution is characterised by scale-invariance. In fact, the very name — ‘power’ in ‘power law’ — relates to the exponent in fractals, i.e., fractal dimensions (also called Hausdorff dimensions). Fractals are defined through recursion and scale-invariant structures. As a result, probabilities do not fall disproportionately for events with ever-increasing extremity.
In both cases, as extremity rises, probability falls (of course) — the difference is that this decrease in probability is disproportionate and exponential in a normal distribution but not in a power law distribution.
Thinking back to expected value,
In a normal distribution, expected value falls as extremity of an event rises (since the decrease in probability offsets the increase in extreme payoffs)
In a power law distribution, expected value rises as extremity of an event rises (since the increase in extreme payoffs offsets the decrease in probability)
This, then, is a slightly technical way of reasoning to illustrate the same idea: betting on outlier Black Swans is a favourable strategy in power law distributed systems, though not in normally distributed ones.
Worldviews
Optimism and pessimism are self-explanatory. A definite world is where one has firm convictions and systematic plans. An indefinite frame is one where no concrete measures are taken to transform the optimistic or pessimistic worldview into reality.
Since Black Swans are relative to expectation — what is a Black Swan for the hypothetical turkey is not a Black Swan for the butcher — definite optimists are well-prepared for outlier events, while indefinite optimists are exposed to negative Black Swans.
By the way, I hypothesise that these philosophical worldviews are linked to world orders (as described in Ray Dalio’s Principles For Dealing With The Changing World Order) — I hypothesise that definite optimism is linked to a favourable world order position (e.g., USA in the 1950s).
There are a whole host of ideas that I’ve skipped here for brevity’s sake: redundancy as a hedge against fragility, Popper’s fundamental unpredictability, barbell strategy, evidence of no disease ≠ no evidence of disease, the equivalence between predicting a random variable and guessing a nonrandom-but-unknown variable, and much more.
Feedback and reading recommendations are invited at malhar.manek@gmail.com